Some time ago
I wrote about a routine to calculate the closest distance to a quadratic bezier spline and recently I reused this routine again in a slightly optimized form to create
wiggles.
Being able to calculate the closest distance to a quadratic spline is useful but I really wanted to use
cubic splines because they offer more control, allowing for easier ways to create nice shapes.

update: made the code 10% faster by making it 2D only. The GitHub version relects that change but original code can be used by removing a single macro
Warning; long read ahead :-) The first section describes how to use the shader and where to download the code and is pretty short. The second section dives deep into the code and is definitely not an easy read, sorry for that but fortunately there is no need to go that deep if you know what a cubic spline is and just want to use the code.
If you would like to know more about programming OSL you might be interested in my book "Open Shading Language for Blender". More on the availability of this book and a sample can be found on
this page.
The shader
The approach to finding the distance to a cubic spline is the same in principle as for a quadratic spline: find all values for
t that satify the relation
dB(t)/dt . (B(t) - P) = 0, or in English: those values of
t whre the tangent to the spline is perpendicular to the vector pointing to the point being shaded (remember that the dot product of two vectors is zero if they are perpendicular).
For a quadratic bezier curve the equation to solve is cubic and is quite simple but for a cubic bezier curve this is a fifth order equation for which there is no analytical solution. And although cubic splines are used everwhere (for example in fonts) a numerical solution for this problem was surprisingly hard to find.
Fortunately after some serious searching the
Graphic Gems series of books proved again to be incredible useful, specifically "A Bezier Curve-Based Root-Finder" by Philip J. Schneider.
The
original code is in C so it neede quite some work to convert it to OSL. Normally converting C code to OSL is pretty straightforward but this code uses multidimensional arrays and recursion, both unknown to OSL. On the plus side, OSL's native
point type and built-in
dot() make for a lot less code.
Code availability and node setup
My implementation (with a sample shader in the same file) is available on
GitHub. The node setup used to create the heart shape is shown below, it is made of two mirrored splines:
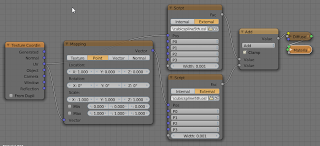
The values for the control points are:P0 = ( 0.5, 0.1, 0.0)
P1 = (-0.5, 0.7, 0.0)
P2 = ( 0.4, 1.2, 0.0)
P3 = ( 0.5, 0.8, 0.0)
Code explanation
I am not going to list all of the code because it's way to long and rather boring but I will tell some more about the
FindRoots() which is nontrivial and needed to be reimplemented in a non-recursive form.
The general idea of the shader to cast the fifth order equation whose roots we'd like to find in a form that is itself a bezier curve (I.e. a
bernstein polynomial) and exploit the specific properties of a bezier curve to efficiently find the roots.
The mathematical specifics are explained very well in Schneider's article so let us just look at the code:
#define POP wtop+=6;wn--
int FindRoots(point w0[6], float t[5]){
point w[STACKSIZE];
int wtop=0;
int wend=0;
int wn=0;
for(int k=0;k<6 br="" k="" w0="" w="" wend=""> wn++;
int nc=0;
while(wn>0){
//printf("[%d]",wn);
int cc=CrossingCount(w,wtop); // w[:5]
if(cc==0){
POP;
continue;
}
if(cc==1){
if(wn>=MAXDEPTH){
t[nc++]= (w[wtop][0]+w[wtop+5][0])/2;
//printf(" MAX ");
POP;
continue;
}
if(ControlPolygonFlatEnough(w,wtop)){ // w[:5]
t[nc++]= ComputeXIntercept(w,wtop);
//printf(" FLAT (%.1f | %.1f)",w[wtop],w[wtop+5]);
POP;
continue;
}
}
// not flat or more than one crossing
DeCasteljau(w,0.5,wtop,wend); //left=[wend:wend+5], right=[wend+6;wend+11]
for(int k=0;k<6 br="" k="" w="" wend="" wtop=""> wn++; wend+=6;
}
return nc;
}
A fifth order bezier curve has 6 control points and at most 5 roots. The control points are passed as the
w0 argument and the
t array will receive the root values. The function's return value will be the number of roots found.
The central idea of this algorithm is to find a segment of the curve that crosses the x-axis just once and then determine the intercept, i.e. a root. To achieve this the spline is subdived into to halves, each again a fifth order spline, until such segment contains a single crossing.
Because OSL doesn't support recursion, we have to maintain a stack of control points ourselves and that's where the
w array comes in.
Starting with the for-loop in line 8 we transfer the initial set of 6 control points to the stack and adjust
wn to reflect that we now have one set on the stack. At this point
wtop (the index of the first control point in the topmost set) is 0, and
wend (the index of the first free slot in
w) is 6.
nc holds the number of roots found sofar.
Next we iterate as long as there is a set of control points on the stack (line 11). We caculate how many times the curve defined by this set crosses the x-axis. If there is no crossing there is no root in this curve so we pop the set of the stack and continue.
If there is a single root and we have recursed deep enough we simply approximate the root as lying halfway between the x-coordinates of the first and last control points and pop the set (line 20). If there is room to recurse we check whether the set of control points is "flat enough" (line 25) and if so compute the intercept with the x-axis of the line between the first and last control point. We store this root and pop the set of control points (see Schneider's article or the original source code to see what is meant by "flat enough").
If the control points are not "flat enough" or we have more than one root in this curve, we split the curve in two using
DeCasteljau's method (line 33). The function will produce two sets of six control points at position
wend in the
w array. The save space we copy the second set to top of the stack (because the control points for the original curve are no longer needed), which means we only have to increase the stacksize
wn by one.
Finally, if we run out of the while-loop we simply return the number of roots found.
Speed
Now you might think that all this recursion and the numerous calculations would be very slow but you will be surprised. The function seldom needs to recurse very deep because the accuracy used to determine if a curve is "flat enough" need not be that good (we can't see differences much less than a pixel). On my machine this means that I can tweak the node setup for the example image at interactive speeds if I set the number of preview samples to 1.
There is however plenty of room for optimization, especially in areas were we do calculations with 3D points. If we only want to work in 2D we might save up to 30% on unnecessary calculations.








