Lenticular printing
The idea of providing a different image based on the viewing angle is not new and is fact readily available in traditional media under the name Lenticular printing. But in OSL we are able to act on any incidence vector, not just the one from the camera. This means for example that shadow rays act as they should and that we can make our material transparent in places to let it cast correct shadows.
But in OSL we are able to act on any incidence vector, not just the one from the camera. This means for example that shadow rays act as they should and that we can make our material transparent in places to let it cast correct shadows. In the sample image and in the video we used this trick to render venetian blinds as seen from different position with just s single plane.
The concept is simple: the horizontal slats of the blinds appear taller when seen from an angle so we calculate the angle between the incidence vector and the x-axis (because unfortunately there is no attribute
object:rotation to determine the up axis of an object) and divide that by maximum angle that would let us see something through the blinds. That fraction is used to paint part of a horizontal strip representing a slat. Finally we replace the shading normal by one that is perpendicular to the slat allowing for s bit of a curve across the slat:
surface venetianblinds(
point Pos = P,
float Spacing = 0.1,
float Width = 0.1,
float Curve = 0.2,
output float Fac = 0,
output float Top = 0,
output normal Normal = N
){
Top = dot(I,vector(0,0,1))>0;
float maxangle = atan(Spacing/Width);
float angle = abs(M_PI_2-acos(dot(normalize(-I),vector(0,0,1))));
float height = Spacing;
// TODO we should look at the sign here to prevent 'flip'
if (angle < maxangle){ height *= angle/maxangle; }
float z = mod(Pos[2],Spacing);
Fac = (z < height);
if(z< height){
Normal = normalize(vector(0,0,1)+N*Curve*(height/2-z)/height);
}
}
Example node setup
The node setup used to render both the still and the video looks like this: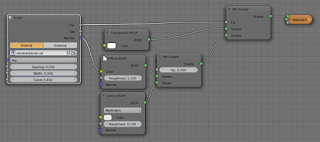 This material is applied to a simple plane. The lighting consists of a single mesh light on the left.
This material is applied to a simple plane. The lighting consists of a single mesh light on the left.



