NodeSet Pro ported to Blender 2.80

NodeSet Pro has now been ported to Blender 2.80 and is available from BlenderMarket.
Porting this add-on has been fairly easy but be aware that Blender 2.80 is still in beta so you might encounter difficulties!

Blender add-on: TextureWatch

I am happy to announce that yesterday I published my new TextureWatch add-on on Blendermarket.

As illustrated in the video, TextureWatch is a small add-on to automatically synchronize textures used in your .blend file if they change on disk. This simplifies working with external programs like Gimp or Substance Painter because TextureWatch can automatically update those textures when you save your files without the need to go through all images inside Blender one by one and selecting reload. This saves time as well as guarantees consistency.

If you find this useful you might want to take a look at my BlenderMarket store.

Extending the Voronoi node in Cycles: a progress report

In a previous post I reported on a small project to extend the functionality of the voronoi noise node in Cycles. After some discussion with developers and users, I spent some time on it and the basic code is done.

Basically the Cycles Voronoi texture node will have all the functionality of its Blender Internal counterpart: you can choose different metrics (= ways to define what a distance is) including the manhattan and chebychev metrics and you can choose whether you want to closest neighbor, the 2nd closest (and 3rd, 4th) or the difference between the 2dn and the 1st closest (a.k.a. Voronoi Crackle). A sample is shown below:

The node has the same outputs as before and just has two extra buttons and an extra input socket (E, which controls the exponent of the Minkovski metric):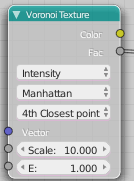

The node defaults to the old options and produces output that is pixel for pixel identical to the old output (with a distance metric of Distance squared). The downside of all this extra functionality is that it is slightly slower (because it now has to choose between different metrics and has to keep around more data). So currently I am checking if or where it makes sense to optimize the code some more. I don't want to complicate the code too much because that would make both maintaining and reviewing the code harder, so at this point it might be more sensible to let it be and accept a few percent penalty for now.

Fast Voronoi F2F1 in Blender Cycles on GPU and CPU

The voronoi noise texture in Blender Cyles is rather limited: it is only based on the distance to the nearest point while many interesting patterns need the distance to the next nearest points as well (or the difference F2 - F1). Also there is no way to vary the distance metric, everything is based on the distances squared while for example so called manhattan metrics yield squarish patterns that can be quite useful.

I did submit the path for review just now, if you're interested you can follow its fate here.

All of this can be overcome by using Open Shading Language, but the Cycles OSL implementation is limited to the CPU and cannot benefit from a much faster GPU. I therefore decided to try and implement it in the Blender source code and that went rather well (but see my rants below):

As you can see I added a second value output to the Voronoi node that yields the distance to the next nearest neighbour and added a dropdown to select the distance metric. Currently I have implemented the distance, distance squared (the default), manhattan and chebychev metrics, I might add the generalized minkowsky metric as well. The images show the F2 - F1 noise for the distance squared and manhattan metrics respectively:

The code works on GPU and on CPU but I only tested it on 64bits Linux (Ubuntu 15.04 to be precise) although there is no reason to believe it will work differently on antoher OS.

Can I haz codez?

The diff to the Blender source code as of 8/8/2015 is for the time being available via DropBox. If there is enough positive feedback I will try to get the patch accepted for inclusion in the source code. Note that the diff shows also some changes to files that have nothing to do with the node itself, notably device_cuda.cpp, which i need to tweak because although I have a GTX970 (= SM_52 capable) card, I didn't upgrade my cuda drivers so i needed to hack the source to restrict the cuda compiler to sm_50. This is irrelevant to the patch itself.

Some remarks about the code: coding this was not all pleasure and that is an understatement. No less than 8 files needed to be changed to alter a single node type. That isn't a bad thing in itself but there is duplicated code, a lot of redundant constants defined in different places and I could find no decent documentation on the stack based virtual machine (svm) that is used by Cycles. It took me way longer to fathom the ins and outs of the code than it took to write the code itself and I am still not 100% certain that I did not miss something. Blender is a wonderful piece of software but it certainly would benefit from a set of decent architecture docs :-)

Irregular stone patterns in OSL, a first attempt

On the BlenderArtists forum a member was analyzing irregular stone walls and posed the interesting question: does this resemble a tree pattern and can it be done in OSL? Quite a lot of thinking and tinkering is needed for a full solution put in this post we explore some of the basic requirements.

Irregular stone patterns

A sample pattern with primary colors, Mondrian eat your heart out :-)
The sample image shows that we have generated a pattern consisting of rows with different heights, each consiting of stones of varying width. Additionally, some stones within a row are further split horizontally. The code to generate the pattern is shown below:

shader stones(
  point p = P,
  vector Scale = 1,
  float w = 0.02,
  float s = 2,
    
  output float Fac = 0
){
  point Pos = p * Scale;
  
  float bot = floor(Pos[1]-1)+cellnoise(Pos[1]-1);
  float lev = floor(Pos[1])+cellnoise(Pos[1]);
  float top = floor(Pos[1]+1)+cellnoise(Pos[1]+1);

  if( Pos[1] < lev ){
    Pos[0] += s*cellnoise(Pos[1]);
  }else{
    Pos[0] += s*cellnoise(Pos[1]+1);
  }
  float left = floor(Pos[0]-1)+cellnoise(Pos[0]-1);
  float mid = floor(Pos[0])+cellnoise(Pos[0]);
  float right = floor(Pos[0]+1)+cellnoise(Pos[0]+1);
  if( 
    ((Pos[0] > left+w) && ( Pos[0] < mid - w )) 
    || 
    ((Pos[0] > mid+w ) && ( Pos[0] < right - w))
  ){
    if( 
      ((Pos[1] > bot+w) && ( Pos[1] < lev - w )) 
      || 
      ((Pos[1] > lev+w ) && ( Pos[1] < top - w))
    ){
      int stoneindex=0;
      float seeda = left;
      float seedb = bot;
      float bounda = mid;
      float boundb = lev;
      
      if( Pos[0] > mid ){ stoneindex += 2; seeda = mid; bounda = right; }
      if( Pos[1] > lev ){ stoneindex += 1; seedb = lev; boundb = top; }
      int pattern = (int)floor(cellnoise(seeda,seedb)*4);
      if( pattern == 0 ){
            // horizontally halved
            float nlev = (seedb + boundb)/2;
            if( (Pos[1] > nlev - w) &&  (Pos[1] < nlev + w) ){
              Fac = 0;
            } else {
              Fac = cellnoise(vector(seeda,seedb,Pos[1]>nlev));
            }
      } else {
        Fac = cellnoise(vector(seeda,seedb,-1));
      }
    }
  }
}

(The code is also available on GitHub.)

Sample node setup

The example image at the top of this article was made with the following node setup (click to enlarge)
:

Further work

Obviously we need more sub patterns for the individual stones and add some distortion to the underlying coordinates to make really random stones. It would probably also be a good idea to vary the spacing between the stones and use the output value to drive displacement and bump maps and the code could certainly do with a bit of cleanup but I thinks this approach is at least shows promiss.

Book review: Blender 2.6 Cycles: Materials and textures cookbook

Last week I had the opportunity to read the Cycles materials and textures cookbook and it proved to be a worthwhile read.

The author, Enrico Valenza, is an experienced and professional Blender user so a book by him is certainly worth checking out. The book presents some thirty shaders in a cookbook style and offers many insights in the Cycles rendering system not limited to specific materials. Although a cookbook implies that you can use the recipes as they are presented, the techniques that are offered in the book will get you a lot further than that and will help you develop skills necessary to develop your own materials because of the very detailed way their implementation is described.

pros

thorough,

each material is described in step-by-step detail and pretty much every avaible Cycles node is featured somewhere and both node groups and frames are covered as well,

comprehensive,

both materials based on textures and materials based on procedural noise are covered and the all important concept of layering increasingly fine detail to get realistic textures is featured quite some times,

interesting

some materials feature mainly as a means to illustrate a concept but many materials are quite good and some are even excellent, my favorites are the sponge texture, the leather texture and the ancient bronze texture.

cons

• the introductory chapter on how to set up Cycles and where to find stuff isn't all that clear. This isn't necessarily the author's fault because sometimes the Blender interface can be overwhelming. Maybe this is one of those situations where a video tutorial is useful,
• the resolution of the illustrations is way to low. If you try to zoom in the lettering of the node labels isn't readable. And yes, high resolution versions of those illustrations are available for download but that detracts from the reading experience a lot.

Conclusion

Nice and thorough book to get you started on creating materials for Cycles, the e-book versions are certainly worth your money in my opinion (personally i think that twice the price for a print version is over the top but of course there will always be people who prefer the genuine touch of paper :-)

Rayleigh scattering in Cycles

Prompted by a question in a comment by Joakim Poromaa Helger I came up with this approach to emulate Rayleigh scattering (the effect that turns the sky blue and the sun red at the same time) in Cycles: by combining a transparent and a glass shader.

In the picture above there is a bright white sun on the right. In a material that exhibits Rayleigh scattering (like air) blue light is scattered more than red light. That means that light traveling from a lightsource through such material will be tinted red because blue light is scattered to all sides. In a direction away from the direct path of the light we see just this scattered blue light and not (or much less) the direct light.

Now if we combine a red(ish) transparent shader with a blue(ish) glass shader, the transparent shader will cause some of the light to be passed through the object without regard for index of refraction and give it a redish hue, while the glass shader will pass some (refracted) blue light through and reflect some. (In the sample picture I have turned off caustics because that takes forever to give a good quality render but also because in this setup caustics exhibit a blue color while it should be redish as well). The node setup looks like this:

With some extra trickery we can correct the color for any caustics as well:

(Note that this image took 10,000 samples and the caustics are still very noisy. Clearly caustics is not Cycles strong point. The light/shadow inside the orb are due to the fact I placed it slightly below the ground but am to lazy to fix it).

We achive the caustic coloring by arranging that the camera sees the blue glass shader while any object receiving diffuse light (like the floor) sees a red glass shader, a distinction we can make with help of the light path node:

Now obiously the effect here is exagerated for demonstration purposes and arguably it is not a real simulation of Rayleigh scattering but for artistic purposes this might be a good start.

A fabric shader using Gabor noise

A combination of two perpendiclar anisotropic Gabor textures is an easy way to create textures that mimic fabrics. In this post we use this to create a simple denim fabric.

In a previous post I presented a simple node to provide Gabor noise. Anisotropic Gabor noise with a large direction vector has slightly undulating parallel lines. Two of these perpendicular to each other are an easy way to create a fabric like structure.

(Click to enlarge if you cannot see the individual threads of the fabric)

The material that is presented here is probably not as versatile or fast as the fabric node I presented earlier, but it does give a somewhat more natural result (at least in my opinion) and is foremost an example of how versatile Gabor noise is. Also, because a Gabor noise node is farly high on the todo list for Cycles this means in the future we might not be dependent on custom nodes as presented here.

Example node setup

The node setup here isn't exactly pretty (click to enlarge) but the main idea is the combination of two Gabor noise nodes (show in a previous post):

As indicated in the image both nodes have a fairly large direction vector which gives small lines. Both vectors are prependicular. The resulting noise is a value that may be less than zero and adding a value to the result as we do here allows for control over the apparent gap between the threads of the fabric. A hight value gives less visible space between the threads. Note that the scale value on the left controls the scaling of the UV-space. It has an effect on the variation of the noise but not on the number of threads per centimeter, that is completely controlled byt the direction vectors. The bandwidth value controls the quality: changing it gives less or more of a 'fluffy' appearence to the threads.

A Chainlink Fence OSL Shader for Blender Cycles

A simple shader to generate a chain link fence pattern that shows that a little displacement can go a long way.

The example image was again generated using one of Bob Groothuis excellent HDRI maps from his Dutch Skies collection. The concrete texture in the front is from www.cgtextures.com

The whole trick in generating a chain link fence pattern is realizing there is a lot of symmetry involved so we only need to think about the calculations for one part.

#include "stdosl.h"

float arc(float x){ return sqrt(1-(x-0.5)*(x-0.5)/0.25); }

shader chainlink(
 point Pos = P,
 float Width = 0.05,
 output float Fac = 0,
 output float Displ = 0
){
 float x = mod(Pos[0],1);
 float y = mod(Pos[1],1);
    float ox = x ;
    float oy = y ;
    x += Width * (0.5 - oy );
    y -= Width * (ox - 0.5 );
 if ( y > 0.5 ){
  y = 1 - y;
  x = 1 - x;
 }
 if ( x > 0.5 ){
        if ( y > 0.5 - Width ){
   Fac = 1;
   Displ = arc((y-(0.5-Width))/Width);
  }else if (x < 0.5 + Width) {
   Fac = 1;
   Displ = arc((x-0.5)/Width);
  }
 }else{
  float r = hypot(x-0.5,y-0.5);
  if (r < Width) {
   Fac = 1;
   Displ = arc(r/Width);
  }
 }
}

The symmetry trick is in lines 17 - 20 where we invert the right half of a square around the center. The way we generate our pattern would cause the ends of the wires at the edges of the square not to line up so in line 15 an 16 we skew the grid a bit to correct this. this extra work before hand makes generating the wires of the chain link fence now very straight forward,

Example node setup

The way to use this shader is by using a default (aka reset) uv map from a simple plane and scale/rotate it as you see fit. The node setup shown here is about the simplest you can get: we simply map the Fac socket to a mix shader to map between a fully transparent shader and a material, in this cas a node group that implements some simple rather dull metal (not shown here). The caclculated displacement is directly plugged into the material output node and thereby converted to a surface normal but we could have used a bump node as well.

Note that although hardly visible in the ambient lighting of the example image, our material does cast nice shadows.

A Fabric OSL shader for Blender Cycles

In this post I present a simple shader that creates fabric or weave patterns.
The shader that is shown in the code below is not only capable of creating simple over-under patterns but also so called twill patterns. Its application is of course not limited to just fabrics, you could use it for baskets made of spliced bamboo for example or a divider made of hazel twigs.

The code for the shader is as often quite simple:

// greatest common divisor
int gcd(int A, int B){
    int a=A, b=B;
    if (a == 0) { return b; }
    while (b != 0) {
        if (a > b) {
            a = a - b;
        } else {
            b = b - a;
        }
    }
 return a;
}

// smallest common multiple (assumes a, b > 0 )
int scm(int a, int b){ return a*b/gcd(a,b); }

shader weave(
 color WarpColor = color(0.8,0,0),
 color WeftColor = color(0,0.8,0),
 int skip = 1,
 int underrun = 1,
 int overrun = 1,
        float WarpWidth = 0.8,
        float WeftWidth = 0.8,
 vector Coordinates = 0,
 output color Color = 0,
 output int Index = 0,
        output float Dist = 0
)
{
 int ny = underrun + overrun;
 int nx = scm(skip,ny);
 
 float x = mod(Coordinates[0],1.0);
 float y = mod(Coordinates[1],1.0);
 
 int ix = int(floor(x*nx));
 int iy = int(floor(y*ny));

        float cx = mod(x*nx,1.0);
        float cy = mod(y*ny,1.0);
     
 int top;
 top = ((iy+skip*ix)%ny) < overrun;

        float lx = (1-WarpWidth)/2;
        float hx = 1-lx;
    float ly = (1-WeftWidth)/2;
    float hy = 1-lx;

    if (top) {
        if ( cx > lx && cx < hx ){
            Index = 1;
            Color = WarpColor;
            Dist = abs(0.5-cx);
        } else if (cy > ly && cy < hy ){
            Index = 2;
            Color = WeftColor;
            Dist = abs(0.5-cy);
        }
    } else {
        if (cy > ly && cy < hy ){
            Index = 2;
            Color = WeftColor;
            Dist = abs(0.5-cy);
        } else if ( cx > lx && cx < hx ){
            Index = 1;
            Color = WarpColor;
            Dist = abs(0.5-cx);
        }
    }    
}

You may experiment with the skip, overrun and underrun values to get different patterns. The only real trick is to determine if we should display the vertical thread on top or the horizontal one. This is done in line 45. The rest of the code then simply checks whether we are withing the width of a thread.

Example node setup

The shader may be straightforward, the node setup used to create a canvas (or burlap) like appearance is less so because we need to introduce a certain amount of color variation inside the individual fibres and make sure that we have transparency in between the fibres (click to enlarge):

Future steps

As I am convinced Blender could benefit from an extensive set of very basic patterns that can be reused, I think I'll focus on a polkadot pattern for a next article.

A soap bubble OSL shader for Blender

The next step in our yourney to develop useful OSL shaders is a soap bubble shader.

The color patterns in soap bubbles and oil films are caused by a phenomenon called thin film interference. Our goal is to recreate those color patterns in a more or less physically accurate way.
Unlike the scales and hexagon shaders we developed earlier, this shader does not simply generate a color pattern but produces colors that are dependent on the angle of incidence. Because the incidence vector I is already provided in OSL as are many vector operations, this irridescence shader is surprisingly simple to implement.

surface irridescence (
 float nmedium = 1, // approximate refractive index of air
 float nfilm   = 1.3, // approximate refractive index of water
 float d       = 1000, // 1000 nm = 1 micron
        output color Color = 0
)
{
 // condition for constructive interference:
 // 2 * nfilm * d * cos(t2) == (m-0.5)*lambda
 // d and lambda in nm
 float eta = nmedium/nfilm;
        // note that N should be the perturbed normal
 vector T = normalize(refract(I,N,eta));
        // no need to divide by (len(-I) * len(T)) as these are normalized
 float cost2 = dot(-I , T);
 float opd = 2*nfilm*d*cost2;

 int mmin = int(ceil(opd/750+0.5));
 int mmax = int(floor(opd/350+0.5));
        // if mmax < mmin the film is too thin to show an effect
 int m = (mmin + mmax)/2;

 if (m > 0){
     float lambda = opd / (m - 0.5);
            color c = wavelength_color(lambda);
            Color =  c;
 }
}

In the code shown above the trick is that we calculate the length of the optical path opd first and then (in line 18) calculate the minimum and maximum number of wavelengths (plus a half to correct for a phase shift, check the Wikipedia article to see why) that fit in this path. The minimum number of wavelengths is calculated by dividing by the wavelength of the longest waelength we can see (red, 750 nm), the maximum by dividing by the shortest wavelength (blue, 350 nm). If the film is too thin, mmin will be smaller tban zero.
The next step is to pick any integer that lies between those extremes (line 21) and calculate the wavelength lambda that corresponds with this integer (line 24). The final trick is converting this wavelength to a RGB-color with OSLs built-in wavelength_color() function.

Example node setup

The shader produces 'just' colors so it is best to combine plug it into a glossy shader and combine it with a general glossy shader too make things resemble a soap bubble. In the node setup shown below we've thrown in some noise to perturb the normal so we get the characteristic color swirls we see in real life soap bubbles.

Future steps

The next article in this series will probably cover weave patterns.

A Toon OSL shader for Blender

A question on Blender Artists made me think about a toon shader. There are of course many ways to implment toon shaders but here is what I came up with.

The basic idea of this shader is to determine how perpendicular the surface of an object is compared to the viewing angle and return black instead of the regular color if some threshold is passed. That is exactly what line 8 does in the code below.

shader outline(
    color Color = 1,
    float Angle = 50,
    output color Cout = 0
)
{
    float angle = cos(radians(Angle));
    if(abs(dot(-I,N)) > angle) Cout = Color;
}

Example node setup

The noodle used to create the sample image of Suzanne looks like this:

A Scales OSL shader for Blender

The second OSL shader I have implemented for Blender is a scales pattern. It provides an overlapping pattern of semicircles that can be used for things like fish scales or roof shingles.

Like the hexagon shader this is a generic shader, i.e. a shader that provides a color pattern irrespective of lighting conditions so it is possible to use it in different contexts. In the code shown below the shader is defined with two input colors, coordinates (typicallt uv-coordinates of the object) and a parameter called n which can be used to alter the shape of the scales.
Beside a color and an index we provide an output for the distance to the center of a scale (which can be used for nice displacement effects) and a vector Vindex which is unique for each scale but the same within the scale. This can be plugged into a texture to provide each individual scale with its own distinct color. In the example noodle for the image shown at the beginning you can see how this is done.

shader scales(
    color Diffuse_Color1 = color(0.2, 0.8, 0.2),
    color Diffuse_Color2 = color(0.8, 0.2, 0.2),
    vector Coordinates = 0,
    float n = 0,
    output color Color = 0,
    output int Index = 1,
    output float Distance = 0,
    output vector Vindex = 0)
{
    float sx = mod(Coordinates[0],1);
    float sy = mod(Coordinates[1],1);
    
    vector p  = vector(sx,sy,0);
    vector p0 = vector(0.5,0,0);
    vector p1 = vector(0.5,1,0);
    vector p2 = vector(0,0.5,0);
    vector p3 = vector(1,0.5,0);
    
    vector cell = vector(floor(Coordinates[0]),floor(Coordinates[1]),0);    
    int oddx = int(cell[0])%2;
    int oddy = int(cell[1])%2;
    
    float dist(vector a, vector b, float n){
        float x = b[0]-a[0];
     float y = b[1]-a[1];
     float r2 = x*x+y*y;
     if ( n != 0.0 ) {
            float theta = atan2(y,x);
         float cost, sint;
            sincos(theta, sint, cost);
         float cost2= cos(theta*2);
         float Y = pow(abs(sint),1+n*(1-cost2*cost2));
         r2 /= cost*cost+Y*Y;
        }
        return sqrt(r2);
    }
    
    float d1 = dist(p,p0,n);
    if ( d1<=0.5 ){
        Color = Diffuse_Color1;
        Index = 0 ;
        Distance = d1;
        Vindex = cell + p0;
    } else {
        float d2 = dist(p,p2,n);
        float d3 = dist(p,p3,n);
        if ( d2 <= 0.5 ) {
            Color = Diffuse_Color2;
            Index = 1;
            Distance = d2;
            Vindex = cell + p2;
        } else if ( d3 <= 0.5 ) {
            Color = Diffuse_Color2;
            Index = 1;
            Distance = d3;
            Vindex = cell + p3;
        } else {
            Color = Diffuse_Color1;
            Index = 0;
            Distance = dist(p,p1,n);
            Vindex = cell + p1;
       }
    }
}

Example node setup

The image of the abstract Koi carp provided at the beginning was created with a node setup that is shown below (click on the image for a larger view):

Future steps

The next shader I will implement I think, will be an irridescence shader so we can all enjoy some soap bubbles.

Example image

Just to illustrate that with scales you do a lot of interesting stuff, here is a picture of the exact same model but with different colors and displacement mapping added to the scales. Looks like a pine cone, right? (Maybe a bit chocolaty one :-)

A Hexagon OSL shader

Now that the Blender Cycles render engine can work with Open Shading Language (OSL) shaders the first task I've set out for myself is to recreate some of the textures I implemented before and the first one we tackle is the hexagon shader.

using an OSL shader in Blender

The hexagon shader in the code below was used to create both the colorfull cube and the chickenwire-like plane in the picture. Provided that you have a Blender build that supports OSL, using the code below requires just two simple steps:

1. Enable the OSL features in the Cycles render settings (the 'Shading syst')
   
2. Load to code below in the text editor

Now you can insert an OSL node anywhere in your node setup by clicking Add -> Script and selecting the name of your text editor buffer in the drop down.

#define A 0.86602540378443864676372317075294 // sqrt(3)/2
#define A2 (2*A)
#define A4 (4*A)
#define SY (1/A)

shader hexagons(
    color Diffuse_Color1 = color(0.2, 0.8, 0.2),
    color Diffuse_Color2 = color(0.8, 0.2, 0.2),
    color Diffuse_Color3 = color(0.2, 0.2, 0.8),
    vector Coordinates = 0,
    output color Color = 0,
    output int Index = 1,
    output float Distance = 0)
{
    // calculate the color
    
    color colors[3] = {Diffuse_Color1,
                       Diffuse_Color2,
                       Diffuse_Color3};   
 
    // we warp the grid so that two adjacent equilateral triangles
    // are mapped to two triangles that fit in a square
    float syc = Coordinates[1] * SY;
    float sxc = Coordinates[0] + 0.5 * syc;
 
    int ind[18] = {1,1,3,3,3,1, 2,2,2,3,3,3, 1,2,2,2,1,1};
 
    int iy = int(mod(syc,3.0));
    int ix = int(mod(sxc,3.0));
    ix = iy * 6 + ix * 2 + ( mod(sxc,1.0) > mod(syc,1.0) );    
 Index = ind[ix];
    Color = colors[Index-1];    
 
    // calculate the distance to the center of the hexagon
       
    float sx = mod(Coordinates[0],3);
    float sy = mod(Coordinates[1]+0.75,A4); 

    // map everthing to a single quadrant
    if ( sx > 1.5 ) sx = 3 - sx;
    if ( sy > A2 ) sy = A4 - sy;
    
    // the distance were interested in is the distance to 
    // the *closest* center point 
    float d1 = distance(vector(sx,sy,0),vector(1.5,A2,0));
    float d2 = distance(vector(sx,sy,0),vector(0,A,0));
    float d6 = distance(vector(sx,sy,0),vector(1.5,0,0));
        
    Distance = min(min(d1,d2), d6);
 
}

The code is a generic shader, i.e. its output color does not take any lighting calculations into account and a more familiar way to refer to such a shader would be a custom texture or pattern. Obviously you can plug its calculated color into a diffuse shader for example but you could also combine it with other textures.
The shader has 3 different colors as input parameters and a coordinate. Its outputs are not only a color, but also an integer color index and the distance to the center of the hexagonal cell. The latter can be used for all sorts of displacement tricks while an index is usefull if you want to change not just the color of a cell but use a completely different texture or shader for each cell.
The noodle for the colorful cube looks like this (click to get a better view):

The noodle for the chickenwire like material looks like this:

Future steps

In the next article I will probably focus on implementing a scales pattern that can either be used for fish scales or roof tiles (shingles).