Each line consists of a number of segments connected end to end. Each segment is angled by a random amount relative to the previous one. Segments are not straight though, but curved by a certain amount. The parameters that control the shape of the line are illustrated below, with on the right an indication of what the basic pattern looks like:
The curved segments are implemented as quadratic splines, using routines discussed in an earlier article.
If you would like to know more about programming OSL you might be interested in my book "Open Shading Language for Blender". More on the availability of this book and a sample can be found on this page.
Code and node setup
The code is pretty straightforward. Apart from a rather long list of input parameters it is mainly concerned with calculating a list of segments for each line we want to draw (there may be more than one per cell). The main trick is in line 86, where we make certain that pointp1, the point that is used to control the curvature of each segment, lies on the line line through the previous control point and the end point. This ensures that each segment joins the previous one smoothly.
#include "equations.h"
#define DOT(a,b) (a[0]*b[0]+a[1]*b[1])
#define SUB(a,b) vector(a[0]-b[0],a[1]-b[1],0)
// determine if point M is inside a rectangle with a margin
int in_rectangle(point M, point a, point b,
vector u, float W, vector v, float linewidth){
point A=a+linewidth*(-u-v);
point B=b+linewidth*(u-v);
point D=B+(W+2*linewidth)*v;
vector AM=SUB(M,A);
vector AD=SUB(D,A);
vector AB=SUB(B,A);
float dotamad=DOT(AM, AD);
float dotadad=DOT(AD, AD);
float dotamab=DOT(AM, AB);
float dotabab=DOT(AB, AB);
return (dotamad > 0 && dotamad < dotadad) &&
(dotamab > 0 && dotamab < dotabab);
}
#define CELL noise("cell", cp, seed++)
#define CELL2 vector(CELL, CELL, 0)
shader wiggles(
point Pos=P,
float Scale=1,
int Number=1,
float Length=0.5,
float LengthVar=0,
float Kink=0,
float Curl=0.2,
float Wave=30, // degrees
int Steps=2,
float StepsVar=0,
float Width=0.02,
float WidthVar=0,
int Seed=0,
output float Fac=0
){
point p = Pos * Scale;
p[2]=0;
point ip= point(floor(p[0]),floor(p[1]),0);
int nn=1+(int)ceil(Steps*Length);
for(int xx=-nn; xx <= nn; xx++){
for(int yy=-nn; yy <= nn; yy++){
int seed=Seed;
point cp = ip + vector(xx, yy, 0);
for(int wiggle=0; wiggle < Number; wiggle++){
vector start = cp + CELL2;
start[2]=0;
vector dir = CELL2 - 0.5;
dir[2]=0;
dir = normalize(dir);
vector perp = vector(dir[1],-dir[0],0);
float k=0.5 + Kink * (CELL-0.5);
float c=Curl*(CELL-0.5);
point p1=start+k*dir+c*perp;
for(int step=0; step < Steps; step++){
vector ldir = dir;
ldir *= Length + LengthVar*CELL;
point end=start+ldir;
if(in_rectangle(p, start, end, dir, c/2, perp, Width+WidthVar)){
float d,t;
if(splinedist(start, p1, end, p, d, t)){
float localwidth = Width+WidthVar*noise("uperlin",start,t);
if(d < localwidth){
Fac = (localwidth - d)/localwidth;
return;
}
}
}
if(CELL < StepsVar){
break;
}else{
p1 = end + (end - p1)*(1+noise("perlin",end)*Kink);
start = end;
dir = rotate(dir, radians(Wave*noise("perlin", start)), vector(0,0,0), vector(0,0,1));
}
}
}
}
}
}
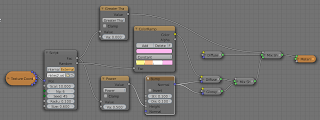
The only other issue that needs attention is the generation of random numbers. In each cell we need a number of them and they need to be unique. We therefore add an extra seed argument to the call to noise. However, we must take care that all those numbers are generated in a repeatable way so we reset this seed for each cell to the value provided by the Seed input. This allows us to generate unique patterns for different objects sharing the same material. The example image at the start was created with a node setup like this:

Note that the
Fac output isn't simply 1 or 0 but contains the distance to the edge of the fiber and we use that to drive a bump node (through a square root math node (power 0.5) to give it a smoothly curved appearance). We use the object info node to generate a random number because the heap of noodles consists of three separate squashed half spheres. The shader expects an integer so we multiply the random value by a million to get a unique integer. One final node of caution: this isn't a cheap shader because calculating the distance to a spline is rather expensive. OSL is quite good at optimizing expressions but still I did dpend quite some time on optimizing the
splinedist() by hand. Did did indeed shave off some small percentage but the biggest win was the conversion of all calculations to two dimensions and the test to see if we are within the bound of the control rectangle before actually checking the distance to the spline (line 72 in the code) A final thing is that most random vectors we generate don't need the z component but OSL has no notion of 2D vectors. I rewrote that in a way that doesn't waste a third of the random values calculated (the CELL2 macro). Even with these optimizations the image with the noodles took an hour to render (200 samples on a hexacore machine). That might be a bit too much but for adding realism to a sweater (in my case that means with cat hairs all over it ;-) this might be a interesting opton.
Code availability
The code is available on GitHub. For ease of use I inlined the necessary functions fromequations.h so the shader can be used as is, without external dependencies.