I took a post on
Blender Artists as a challenge and created a 4D voronoi shader.
Blogspot won't show animated gifs but I put up a short sequence on
PasteAll and if that doesn't work it is also
on my site. In this animated gif, the fourth dimension (time) is animated from 0 to 1 in 50 frames.
The shader presented below is simple enough but convoluted because we cannot manipulate arrays like points or vectors in OSL but otherwise it is a straight forward extension of Blenders bundled voronoi implementation, especially because OSLs cellnoise function supports 4D noise out of the box (you can pass it a point and a float).
#include "stdosl.h"
void cellnoise_color4d(float p[4], float c[4])
{
c[0] = cellnoise(point(p[0],p[1],p[2]),p[3]);
c[1] = cellnoise(point(p[1],p[0],p[2]),p[3]);
c[2] = cellnoise(point(p[1],p[2],p[0]),p[3]);
c[3] = cellnoise(point(p[3],p[1],p[2]),p[0]);
}
/* Voronoi 4D . we always use distance squared as the distance metric */
void voronoi4d(point p, float t, float da[4], point pa[4], float ta[4])
{
/* returns distances in da, point coords in pa and time coords in ta*/
int xx, yy, zz, tt, xi, yi, zi, ti;
float op[4] = {p[0],p[1],p[2],t};
xi = (int)floor(p[0]);
yi = (int)floor(p[1]);
zi = (int)floor(p[2]);
ti = (int)floor(t);
da[0] = 1e10;
da[1] = 1e10;
da[2] = 1e10;
da[3] = 1e10;
for (xx = xi - 1; xx <= xi + 1; xx++) {
for (yy = yi - 1; yy <= yi + 1; yy++) {
for (zz = zi - 1; zz <= zi + 1; zz++) {
for (tt = ti - 1; tt <= ti + 1; tt++) {
float ip[4] = {xx, yy, zz, tt};
float vp[4];
cellnoise_color4d(ip,vp);
float pd[4] = { op[0] - (vp[0] + ip[0]),
op[1] - (vp[1] + ip[1]),
op[2] - (vp[2] + ip[2]),
op[3] - (vp[3] + ip[3])};
// always distance squared
float d = pd[0]*pd[0]+pd[1]*pd[1]+pd[2]*pd[2]+pd[3]*pd[3];
vp[0] += xx;
vp[1] += yy;
vp[2] += zz;
vp[3] += tt;
if (d < da[0]) {
da[3] = da[2];
da[2] = da[1];
da[1] = da[0];
da[0] = d;
pa[3] = pa[2]; ta[3] = ta[2];
pa[2] = pa[1]; ta[2] = ta[1];
pa[1] = pa[0]; ta[1] = ta[0];
pa[0] = point(vp[0],vp[1],vp[2]); ta[0] = vp[3];
}
else if (d < da[1]) {
da[3] = da[2];
da[2] = da[1];
da[1] = d;
pa[3] = pa[2]; ta[3] = ta[2];
pa[2] = pa[1]; ta[2] = ta[1];
pa[1] = point(vp[0],vp[1],vp[2]); ta[1] = vp[3];
}
else if (d < da[2]) {
da[3] = da[2];
da[2] = d;
pa[3] = pa[2]; ta[3] = ta[2];
pa[2] = point(vp[0],vp[1],vp[2]); ta[2] = vp[3];
}
else if (d < da[3]) {
da[3] = d;
pa[3] = point(vp[0],vp[1],vp[2]); ta[3] = vp[3];
}
}
}
}
}
}
shader node_voronoi_texture(
float Scale = 5.0,
point Vector = P,
float Time = 0,
output float Fac = 0.0,
output color Color = color(0.0, 0.0, 0.0))
{
point p = Vector;
/* compute distance and point coordinate of 4 nearest neighbours */
float da[4];
point pa[4];
float ta[4];
voronoi4d(p * Scale, Time * Scale, da, pa, ta);
Fac = fabs(da[0]);
Color = color(Fac);
}
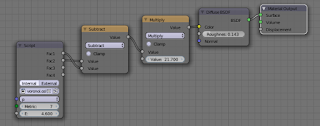
Example node setup
Straight forward enough but note the keyframed Time value.